Copy link
Postextubation Stridor
Last updated: 01/27/2023
Key Points
- Stridor is a clinical diagnosis characterized by a high-pitched inspiratory noise caused by turbulent airflow during breathing.
- Postextubation stridor (PES) typically occurs immediately postextubation, often due to laryngeal edema. Risk factors include difficulty with intubation, tight-fitting endotracheal tube, surgery longer than 1hr, coughing while intubated, and repositioning during surgery.
- Treatment of postextubation stridor includes humidified air, corticosteroids, and consideration for racemic epinephrine in severe cases.
Introduction
Stridor is a high-pitched breathing sound caused by turbulent airflow in a narrowed airway. The obstruction or airway narrowing typically occurs in the larger airways. It is usually inspiratory and is often best heard over the front of the neck. It can be distinguished from wheezing and bronchiolitis, which usually occur during expiration and are best heard lower in the chest.
Stridor can be caused by croup, epiglottitis, foreign body aspiration, airway abscesses (retropharyngeal or peritonsillar), anaphylaxis, anatomic issues (e.g., vascular ring, airway hemangiomas) or iatrogenic events such as postextubation.
PES is a sign of acute upper airway narrowing or obstruction that occurs immediately postextubation. PES in children typically represents laryngeal edema in the subglottic area. Most children with PES are intubated for a medical or surgical procedure with anesthesia. Historically, the incidence of PES in this population was 1%. The incidence is decreasing due to the increased use of cuffed endotracheal tubes (ETT).1 The incidence of PES in children after prolonged endotracheal intubation in the ICU ranges from 4-37%.2
Resistance to Airflow
According to the Hagen-Poiseuille equation, resistance to airflow is inversely proportional to the fourth or fifth power of the radius. Resistance to laminar flow is inversely proportional to the fourth power of the radius, whereas resistance to turbulent airflow is inversely proportional to the fifth power of the radius.3

Hagen-Poiseuille equation
In an infant, 1 mm of circumferential edema in the subglottis decreases the cross-sectional area of the airway by approximately 75% and increases the resistance to airflow (which is usually turbulent) by about 32-fold (Table 1).3

Table 1. Comparison of the effects of airway edema in infants and adults. Adapted from Fiadjoe JE, Litman RS, Serber JF, et al. The Pediatric Airway. In: Cote and Lerman’s A Practice of Anesthesia for Infants and Children. 6th Edition. Philadelphia, PA. Elsevier. 2019. Page 301.
Risk Factors for PES
A retrospective study in the 1970s reported the following risk factors for PES.4
- Age (1-4 years)
- Traumatic intubation or multiple laryngoscopy attempts
- Large ETT or minimal leak around ETT
- Duration of surgery longer than 1hr
- Coughing while intubated
- Position change during surgery
Historically, uncuffed ETTs were used in children younger than 8 years. Due to the narrow cricoid cartilage, there was a concern that cuffed ETTs cause subglottic edema, postextubation stridor, and possibly subglottic stenosis in the long term.
Of note, both cuffed and uncuffed ETTs can cause postextubation stridor. The incidence of PES may be decreasing as the need to exchange the ETT for a different size is decreased when a cuffed ETT is used.
Management
A scoring system for the severity of infectious croup has been developed to guide treatment.5
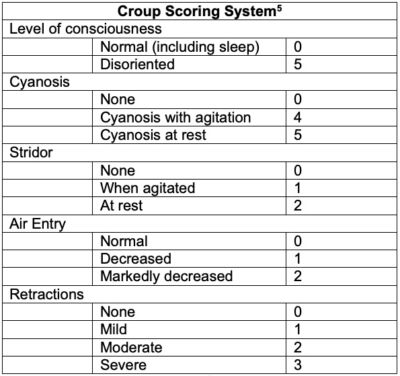
Table 2. Croup scoring system.5
Patients with mild symptoms, a stable airway and a score of 2 or lower can be treated with humidified air or oxygen. Caregivers can also be encouraged to sit with the child in a steam-filled bathroom. While these are treatments traditionally for infectious croup, they can also be used for PES.
Caregivers should be encouraged to watch for nasal flaring, difficulty breathing, cyanosis, retractions and advised to seek medical attention if these occur after discharge.
In a meta-analysis, corticosteroids were found to decrease the rate of PES, upper airway obstruction, and extubation failure in pediatric patients.2 Intravenous dexamethasone may be given prophylactically in the operating room if there were known issues with intubation. Dexamethasone can also be given to treat PES symptoms that occur postoperatively. As it may take some time to work, humified air or oxygen should also be considered until symptoms improve.
Nebulized racemic epinephrine is often recommended in cases of significant stridor. It is thought to work on the ⍺-receptors in the subglottis, causing vasoconstriction and decreasing edema. It works quickly to decrease stridor symptoms and can allow other treatments, such as corticosteroids, time to act. Racemic epinephrine is typically administered as a nebulizer and the dose is 0.05 mL/kg (maximum of 0.5 mL) of a 2.25% solution diluted to 3 mL total volume with normal saline.
The effect of racemic epinephrine often lasts for an hour clinically and is gone in 2 hours. There is a concern for “rebound hyperemia” after the epinephrine wears off and that swelling might be worse than before, necessitating observation for at least 4 hour after nebulizer administration.1 However, a recent study of infectious croup showed that symptoms might recur after the epinephrine wears off, but the symptoms were no worse than before treatment with racemic epinephrine.6
References
- von Ungern-Sternberg BS. Respiratory complications in the pediatric postanesthesia care unit. Anesthesiol Clin. 2014;32(1):45-61. PubMed
- Kimura S, Ahn JB, Takahashi M, et al. Effectiveness of corticosteroids for post-extubation stridor and extubation failure in pediatric patients: a systematic review and meta-analysis. Ann Intensive Care. 2020;10(1):155. PubMed
- Fiadjoe JE, Litman RS, Serber JF, et al. The Pediatric Airway. In: Cote and Lerman’s A Practice of Anesthesia for Infants and Children. 6th Edition. Philadelphia, PA. Elsevier. 2019. Page 301.
- Koka BV, Jeon IS, Andre JM, MacKay I, Smith RM. Postintubation croup in children. Anesth Analg. 1977;56(4):501-5. PubMed
- Westley CR, Cotton EK, Brooks JG. Nebulized racemic epinephrine by IPPB for the treatment of croup: a double-blind study. Am J Dis Child. 1978;132(5):484-7. PubMed
- Sakthivel M, Elkashif S, Al Ansari K, Powell CVE. Rebound stridor in children with croup after nebulised adrenaline: does it really exist? Breathe. 2019;15(1):e1-e7. PubMed
Copyright Information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.