Copy link
Logistic Regression: Odds Ratio
Last updated: 03/03/2015
Regression analysis is concerned with relationship between two or more variables. There are many subtypes of regression depending on the variables to be studied and the nature of the relationship of interest. Logistic (or Logit) regression can be used to investigate outcomes that are binomial or categorical (Mortality vs. Survival, Complication vs. None etc). This can generate a mathematical equation that incorporates these parameters as coefficients to predict probability of the outcome – the regression equation.
Odds take the probability of an event occurring and compare them with it not occurring. An odds ratio is a comparison of odds with a factor present and absent.
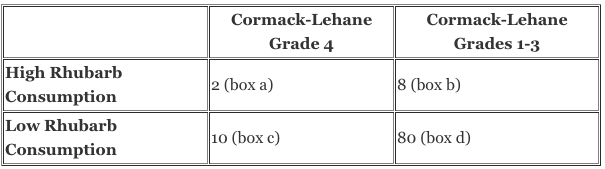
See the image for an(fictitious) example considers a case control trial looking at the presence of a history of high rhubarb consumption and subsequent Grade 4 view on direct laryngoscopy.
The Odds of a History of High Rhubarb Consumption in patients with and without subsequent G4V on Direct Laryngoscopy can be calculated by taking:
1) Odds = a / c = 2 / 10 = 0.2 (Odds of High Rhubarb w/G4V)
The Odds of a Grade 4 view in patients with a elevated serum rhubarb levels can be calculated by taking:
2) Odds = b / d = 8 / 80 = 0.1 (Odds of High Rhubarb w/G1-3V)
The odds ratio is thus:
Odds Ratio = Odds of High Rhubarb w/G4V (from 1) / Odds of High Rhubarb w/G1-3V (from 2)
= a / c = ab
b / d cd
= 0.2 / 0.1
= 2
It can thus be stated that the Odds of a History of High Rhubarb consumption in patients with a G4V is twice that of that in patients with a G1-3V. This is not the same as the risk ratio. The odds of an occurrence are different from the risk of an occurrence. Odds ratios are used in Case Control studies as in this type of study the researcher determines the number of controls to be recruited and thus a true incidence (and thus relative risk) cannot be calculated. The odds ratio may approximate the relative risk when the outcome of interest occurs less than 10% of unexposed people (I,e. Grade 4 view in subjects with low rhubarb consumption).
Logistic Regression allows the determination of the relationship between a number of values and the probability of an events occurrence. The coefficient of this relationship for each factor is the Natural Log of the Odds ratio. A practical application of this point, is that logistic regression techniques allow confidence intervals to be created for multiple odds ratios and thus determination if these factors are statistically significant predictors of outcomes.
References
- Anthony J Viera Odds ratios and risk ratios: what’s the difference and why does it matter? South. Med. J.: 2008, 101(7);730-4 PubMed Link
Copyright Information

This work is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.